
译文/Translated:
介绍
本文我们将介绍支撑REX的Bancor方程式、设置REX初始状态的原因、以及系统中可能存在的约束。我们首先要介绍REX的池余额。我们会用C++智能合约的变量名和方程式中使用的数学变量来表达这些余额。如果没有明确说明,那么所有账户余额、支付费用和储存资源的单位都是区块链核心代币SYS。余额包括
- total_unlent 代表可以租用的SYS余额。在后面的讨论中,我们用u来表示这个余额,即u = total_unlent
- total_lent 代表租用的SYS余额。在任何时候,total_lent 都是现在所有未结贷款中的抵押代币总和。后面我们用l = total_lent
- total_rent 是虚拟余额。如下所示,这个余额的初始值必须是正数。余额total_rent 和total_unlent 是Bancor算法的两个连接器,它们会决定CPU和NET的租金。后面我们用f = total_rent。
关于REX智能合约的详细说明,参考Ref [1]。
REX租赁计算
在租赁CPU或者NET资源时,质押这些资源30天的数量是利用租赁费用函数∆f以及REX池余额u = total_unlent 和 f = total_rent通过Bancor方程式计算获得。Id为i的租赁方程式是
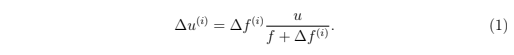
比如,在某个时间点中,u = 5×10⁷, f = 3×10⁴,租赁费用∆f⁽ⁱ⁾ = 1,其结果是租赁费用为∆u⁽ⁱ⁾ = 1666.6111SYS的资源。换句话说,租赁成本率是∆f⁽ⁱ⁾/∆u⁽ⁱ⁾ ≈ 0.06%。一般来说,REX池余额相比给定贷款的费用是比较大的,所以租赁成本率可以被估测为
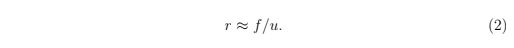
在创建上述租赁时,REX池余额按照下列方式更新:u → u −∆u⁽ⁱ⁾, l → l + ∆u⁽ⁱ⁾, f→ f + ∆f⁽ⁱ⁾。换句话说,质押量被从u移到了l,即,从total_unlent 转到了total_lent。此外,支付费用被加到total_unlent。整个更新如下:
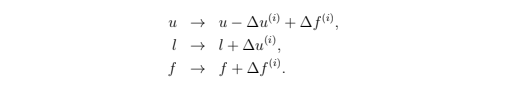
注意,f是虚拟账户,把∆f⁽ⁱ⁾ 加到u和f上不会花费双重费用。
初始化REX池
初始状态下,REX池为空(u = l = 0)。贷方购买REX(借出SYS代币),u增加。另一方面,余额f是虚拟的,需要被初始化赋值f₀。必须注意的是,f₀必须不等于0;否则,不管支付费用有多低,最初的贷款都删掉整个u余额。这可以这么验证:在Eq1中设定f=0,其结果是对于任何∆f > 0都是∆u = u .了解到f₀ > 0,下一步就是给f₀确定实用值。REX池余额预计很快可以达到几千万SYS代币。我们把估计的u₀ = 2 × 10⁷作为参考值。如果很小,它的问题和f₀ = 0一样。比如说,如果f₀ = 100,支付一笔费用∆f = 100带来的租赁质押是∆u = 1 × 10⁷,这就是整个池的一半了。这个过程可以不停地重复,结果就是只要花很小一部分费用就可以租赁到这个池的大部分。在最初的几个租赁之后,成本会迅速上升,变得过高。
另一方面,如果f₀过高,就会导致令人望而却步的高租赁成本。通过设置目标初始租赁成本率r₀ ≈ 0.1%,使用u₀参考余额Eq 2的结果是f₀ = 2 × 10⁴,这就是我们给设置的初始值。
租赁到期
当租赁i到期时,对应的租赁资源∆u⁽ⁱ⁾就被释放了比方说,余额f从total_lent 被转移回total_unlent,其更新方法是减去逆方程的输出
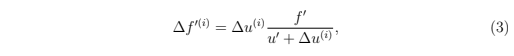
其中∆u⁽ⁱ⁾是通过Eq1计算的,u′ 和 f′ 则是租赁到期时的值。因为这些值一般都和租赁开始时的值不同了,所以f′ ≠ f 以及 u′ ≠ u,于是∆f′⁽ⁱ⁾ ≠ ∆f⁽ⁱ⁾。换言之,Eq3的结果和租赁开始的支付费用不同,简单来说,这些更新是
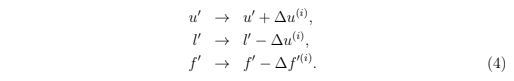
回过头来看Eq3,我们注意到,如果在过期的时候,total_unlent刚好是0(u′ = 0),这个方程就是∆f′⁽ⁱ⁾ = f′。Eq4更新之后,在租赁过期的时候,我们就有了f′ = 0。如上所述,这就导致市场不稳定。可能会导致这个状态的一个原因是这样的:尽管至少存在一个未偿贷款,但是会有不止一个REX所有者可能会大量出售REX,导致total_unlent 跌到u′ = 0。之后,不止一个借贷到期时f′ = 0。为了避免系统遇到这个状态,我们给u设定了一个动态下限,也就是下一节我们讨论的内容。
Unlent balance 下限
设ulb是u的动态下限,即在任意一个时间点内u ≥ ulb。我们必须把ulb定义为只要存在未偿贷款那么ulb > 0,当所有的租赁都到期了,则ulb = 0。第二个版本允许REX所有人出售所有的REX。用l来表示ulb,则在0 <α< 1时,ulb = α×l,这就满足了这两个要求。此外,我们希望ulb是一个合理的低值,这样才不会经常导致销售订单排队、租赁操作失败。比如,设α 0.2,则ulb = 0.2 × l.
注意,我们用l的函数表示ulb而不是用f函数,这里有两个原因。首先,u和f的数量级不同,这就导致两者不可能构成对比。其次,f的值不能用来判断是否存在未偿贷款。
调整REX池的虚拟余额
我们还提供了一个备选方案,当REX的初始条件不平衡时,该方案会被激活。这种情况还是有可能发生的。比如,如果一段时间后,如果total_unlent 还远远低于 上述提到的参考值u₀ = 2×10⁷,这就意味着初始租赁成本率高于目标值r₀ ≈ 0.1%或相似资源租赁市场确定的目标率太多。Setrex这个操作让生产者能把余额f设定成一个由Eq2计算得出的预定值f₀ ≈ r₀ × u,其中u代表着total_unlent 的现在价值,而r₀ 是目标租赁成本率。
方程推导
Bancor协议[2]通过连接了货币储备和智能代币实现了即时流动性,它将准备金率定义为
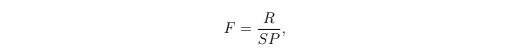
其中R是货币储备的当前价值,S是智能代币的现在储备,P是相对储备货币的当前代币价值。该协议假定F恒定为预定值,该预定值决定了作为供应函数的价格行为。
协议的一个结果是下面这个等式,它表明一定数量的代币要支付的费用
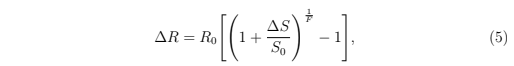
其中R₀是初始储备价值,S₀是初始智能代币供应,∆S 是发行代币的数量
逆方程
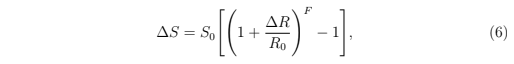
表明一个给定的支付能带发行的智能代币的数量。在代币发行之后,供给就更新到S = S₀ + ∆S ,储备金则是R =R₀ + ∆R。
现在再考虑某智能代币联系两个准备金R⁽¹⁾and R⁽²⁾,并假设该智能代币的部分准备金率相同。支付∆R⁽¹⁾的结果是通过Eq6计算得到的∆S发行的代币应用于R⁽¹⁾:
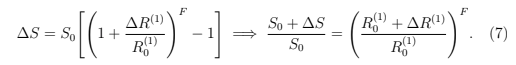
如果出售这些代币(等于把∆S加到智能代币供给中)获得第二个储备金,我们就可以获得
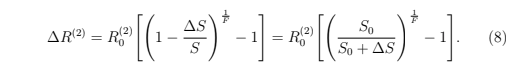
把Eq7导入Eq8,可得
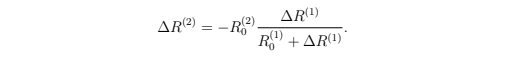
注意,∆R⁽²⁾和 ∆R⁽¹⁾都有反号。在上述REX等式中,两个储备金是f ≡ R⁽¹⁾和 u ≡ R⁽²⁾.
参考文献
[1] REX的应用. https://github.com/EOSIO/eosio.contracts/issues/117 [2] Eyal Hertzog, Guy Benartzi, and Galia Benartzi. Bancor 协议白皮书.所有的产品和公司名都是其相应持有人的商标或者注册商标。使用这些不意味着就和它们有关联或受到其支持。
免责声明
Block.one作为EOSIO社区的一员,自愿做出自身贡献,并不对软件的总体性能及任何相关应用程序负责。对于此处所述版本以及相关GitHub版本或EOSIO软件,我们不作任何明示或暗示的陈述、保证、担保或承诺,包括且不限于提供担保,保证适销性或对某一特定目的和非侵权的适用性,并不承担相应的责任。在任何情况下,无论是合约操作、侵权行为或其他,亦无论是否与软件或文档相关,或由于软件使用导致,或在软件和文档上的其他交易导致的任何索赔、损害赔偿或其他债务,我们均不承担责任。任何测试结果或绩效数据具有指示性,无法反映所有情况下的绩效。任何对第三方或第三方产品、资源或服务的引用都不受Block.one的认可或推荐。对于您使用或信任这些资源的行为,我们概不负责,并且不承担任何责任和义务。第三方资源可能随时更新、变更或终止,因此此处的信息可能已过期或不准确。
原文/Original:
Introduction
In this document, we describe the Bancor equations supporting REX and the reasoning behind setting the REX initial state and any possible constraints on the system. We first present the relevant REX pool balances. These balances are represented both by their C++ smart contract variable names and by the mathematical variables used in the presented equations. If not shown explicitly, the unit of all balances, paid fees and staked resources is the blockchain core token SYS. The balances are
- total_unlent represents the SYS balance that is available for renting. In
the following we use u to represent this balance, i.e., u = total_unlent. - total_lent represents the total rented SYS balance. At any point in time, total_lent is the sum of tokens staked in all currently open loans. In the following we use l = total_lent.
- total_rent is a virtual balance. The initial value of this balance must be strictly positive as discussed below. The balances total_rent and total_unlent are the two connectors of the Bancor algorithm which determines CPU and Network renting prices. In the following we use f = total_rent.
For a detailed description of the REX smart contract, see Ref [1].
REX Loan Calculations
Upon renting CPU or Network resources, the amount staked to those resources for 30 days is calculated as a function of the loan fee, ∆f, and the REX pool balances u = total_unlent and f = total_rent, using Bancor equation. For a given loan with id i, the equation is
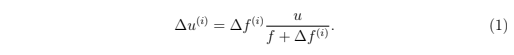
For example, if at a given point in time, u = 5×10⁷, and f = 3×10⁴, a loan fee ∆f⁽ⁱ⁾ = 1 results in renting ∆u⁽ⁱ⁾ = 1666.6111 SYS worth of resources. That is, the renting cost rate for this loan is ∆f⁽ⁱ⁾/∆u⁽ⁱ⁾ ≈ 0.06%. In general, the REX pool balances are large compared to the fee of a given loan, then the renting cost rate can be estimated as
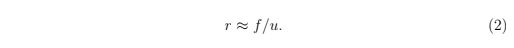
When the loan described above is created, the REX pool balances are updated as follows: u → u − ∆u⁽ⁱ⁾, l → l + ∆u⁽ⁱ⁾, f → f + ∆f⁽ⁱ⁾. In other words, the staked amount ∆u⁽ⁱ⁾ is moved from u to l, i.e., from total_unlent to total_lent. In addition, the paid fee is added to total_unlent. The overall set of updates is
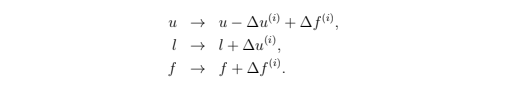
Note that f is a virtual balance and there is no double spending by adding ∆f⁽ⁱ⁾ to both u and f.
Initializing REX Pool
Initially, the REX pool is empty (u = l = 0). As lenders buy REX (lend SYS tokens), u increases. On the other hand, the balance f is virtual and needs to be initialized to some value f₀. It is important to note that f₀ must not be zero; otherwise, the first loan will deplete the entire u balance no matter how small the paid fee is. This can be easily verified by setting f = 0 in Eq 1 which results in ∆u = u for any ∆f > 0. Seeing that we must have f₀ > 0, the next step is to decide a practical value of f₀. The REX pool balance u is expected to reach tens of millions of SYS tokens rather quickly . We will use the estimate u₀ = 2 × 10⁷ as a reference value. A small f₀ causes a problem similar to the one caused by f₀ = 0. For example, if f₀ = 100, a payment ∆f = 100 gives a rented stake of ∆u = 1 × 10⁷, which is half of the entire pool. The same can be repeated and most of the pool can be rented using only a small sum of fee payments. Following the first few loans, renting cost increases rapidly and becomes too high.
On the other hand, setting f₀ to a large value would lead to a prohibitively high renting cost. By setting a target initial renting cost rate r₀ ≈ 0.1%, and using the u₀ reference balance, Eq 2 gives f₀ = 2 × 10⁴, which is the initial value we choose for total_rent.
Loan Expiration
When loan i expires, the corresponding rented resources, ∆u⁽ⁱ⁾, are released,
i.e., moved from total_lent back to total_unlent. The balance f is updated
by subtracting the output of the inverse equation
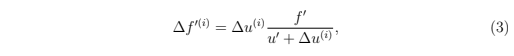
where ∆u⁽ⁱ⁾ was calculated using Eq 1, and u′ and f′ are the values at loan expiration. Since these values are in general different from the values at loan creation, f′ ≠ f and u′ ≠ u, we have ∆f′⁽ⁱ⁾ ≠ ∆f⁽ⁱ⁾. That is, the output of Eq 3 is different from the fee paid at loan creation. To summarize, the updates are
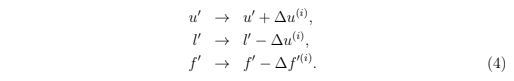
Looking at Eq 3, we notice that if, at the time of expiration, total_unlenthappens to be zero (u′ = 0), the equation gives ∆f′⁽ⁱ⁾ = f′. And following the update given by Eq 4, we get f′ = 0 after the loan expires. As described above, this leaves the market in an unstable state. One scenario that can lead to this state is as follows: while there is at least one outstanding loan, one or more REX owners may sell enough REX to cause total_unlent to drop to u′ = 0. Following that, one or more loans can expire resulting in f′ = 0. In order to prevent the system from reaching that state, we impose a dynamic lower bound on u which we describe in the following section.
Unlent Balance Lower Bound
Let ulb be the dynamic lower bound of u, which means that at any point in time we have u ≥ ulb. We must define ulb such that ulb > 0 as long as there are outstanding loans, and ulb = 0 when all loans have expired. The second condition allows REX owners to sell all their REX. Setting ulb to be a fraction of l, i.e., ulb = α×l, where 0 <α< 1, satisfies both requirements. In addition, we want a reasonably low ulb so that it does not routinely cause selling orders to be queued and renting actions to fail. We set α = 0.2, i.e., ulb = 0.2 × l.
Note that we chose to calculate ulb as a function of l instead of f for two
reasons. First, u is expected to be of a different order of magnitude than f
which makes the comparison impractical, and second, the value of f cannot
be used to determine whether there are outstanding loans.
Adjusting REX Pool Virtual Balance
We provide a backup solution that can be invoked in case REX initial condition is out of balance. This can happen, for example, if after a period of time, total_unlent remains well below the reference value of u₀ = 2×10⁷ described above. It means that the initial renting cost rate is well above target value r₀ ≈ 0.1%, or the target rate determined by similar resource renting markets. The action setrex allows producers to set the balance f to a predetermined value calculated using Eq 2 as f₀ ≈ r₀ × u, where u is the current value of total_unlent and r₀ is the target renting cost rate.
Derivation of the Equations
Bancor protocol [2] allows for instant liquidity by connecting a currency reserve to a smart token. It defines the fractional reserve ratio as
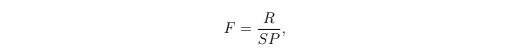
where R is the current value of the currency reserve, S is the smart token current supply, and P is the current token price relative to the reserve currency. The protocol posits that F is always constant and is set to a predetermined value which dictates the price behavior as a function of supply.
One of the results of the protocol is an equation that determines the amount to be paid in return for a given number of tokens:
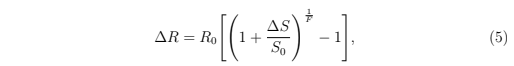
where R₀ is the initial reserve value, S₀ is the initial smart token supply, and ∆S is the number of issued tokens.
The inverse equation,
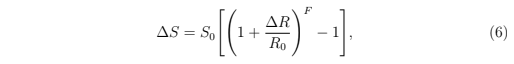
determines the number of smart tokens issued in return for a given payment. After the tokens are issued, the supply is updated to S = S₀ + ∆S and the reserve to R = R₀ + ∆R.
Now consider a smart token that is connected to two reserves R⁽¹⁾and R⁽²⁾, and assume that the fractional reserve ratio of the smart token is the same for both reserves. A payment ∆R⁽¹⁾ results in ∆S issued tokens given by Eq 6 applied to R⁽¹⁾:
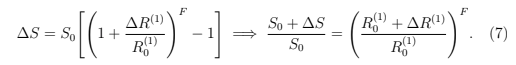
If these tokens are then sold (equivalent to adding −∆S to the smart token supply) in exchange for the second reserve currency, we obtain
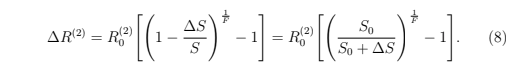
Replacing Eq 7 in Eq 8 results in
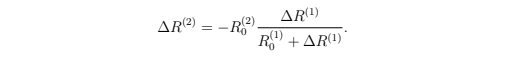
Note that ∆R⁽²⁾ and ∆R⁽¹⁾ have opposite signs. In REX equations shown above, the two reserves are f ≡ R⁽¹⁾ and u ≡ R⁽²⁾.
References
[1] REX Implementation. https://github.com/EOSIO/eosio.contracts/issues/117 [2] Eyal Hertzog, Guy Benartzi, and Galia Benartzi. Bancor Protocol White Paper.All product and company names are trademarks™ or registered® trademarks of their respective holders. Use of them does not imply any affiliation with or endorsement by them.
Disclaimer: Block.one makes its contribution on a voluntary basis as a member of the EOSIO community and is not responsible for ensuring the overall performance of the software or any related applications. We make no representation, warranty, guarantee or undertaking in respect of the releases described here, the related GitHub release, the EOSIO software or any related documentation, whether expressed or implied, including but not limited to the warranties or merchantability, fitness for a particular purpose and noninfringement. In no event shall we be liable for any claim, damages or other liability, whether in an action of contract, tort or otherwise, arising from, out of or in connection with the software or documentation or the use or other dealings in the software or documentation. Any test results or performance figures are indicative and will not reflect performance under all conditions. Any reference to any third party or third-party product, resource or service is not an endorsement or recommendation by Block.one. We are not responsible, and disclaim any and all responsibility and liability, for your use of or reliance on any of these resources. Third-party resources may be updated, changed or terminated at any time, so the information here may be out of date or inaccurate.
原文链接/Original URL: